nitomath’s blog

分からなかったことのメモ

RC回路におけるコンデンサ充電時の電流、電圧、電荷を求める

この記事では、起電力 Eの電源、スイッチ、静電容量 Cのコンデンサ、抵抗値 Rの抵抗が直列接続された回路（RC直列回路）を考えます。 そして、過渡状態における回路を流れる電流、コンデンサの両端にかかる電圧、コンデンサに蓄えられる電荷を求めます。

f:id:nitomath:20200723100727p:plain
RC直列回路

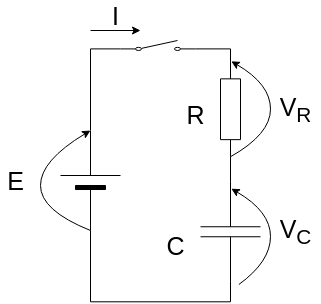
時刻 t=0でスイッチをONにします。 そのとき、電荷 Q=CEがコンデンサに一瞬で蓄えられるわけではありません。 つまり、コンデンサに蓄えられている電荷は

\displaystyle{ Q= \begin{cases} 0~\left( t \lt 0 \right) \\ CE~\left( 0 \leq t \right) \end{cases} }

という式では表せません。

実際には、スイッチがONになってから \Delta tの間、蓄えられている電荷が 0から CEにまで連続的に変化する期間（過渡状態）があります。 つまり、

\displaystyle{ Q= \begin{cases} 0~\left( t \lt 0 \right) \\ Q\left(t\right)~\left( 0 \leq t \lt \Delta t\right) \\ CE~\left( \Delta t \leq t \right) \\ \end{cases} }
\displaystyle{ Q\left(0\right) = 0,~Q\left(\Delta t\right) = CE }

という関数 f\left(t\right)が存在します。 この記事の最終目標はこの関数 f\left(t\right)を求めることです。 そのために、まず過渡状態における電流と電圧を求めます。

電流

過渡状態の電流を I(t)とします。

抵抗による電圧降下を V_R、コンデンサの両端の電位差を V_Cとします。 このとき、電源の起電力が Eなので、キルヒホッフの法則より、

\displaystyle{ E=V_R+V_C }

がなりたちます。

V_Rはオームの法則より、

\displaystyle{ V_R = RI(t) }

なので、

\displaystyle{ I(t) = \dfrac{V_R}{R}=\dfrac{E-V_C}{R} }

コンデンサの両端に V_Cの電圧がかかっているとき、蓄えられている電荷が Q=CV_Cであることと、電荷は電流を時間で積分したものであることより、

\displaystyle{ I(t) = \dfrac{1}{R}\left( E-\dfrac{Q}{C} \right) = \dfrac{1}{R}\left( E-\dfrac{1}{C}\int_0^tI(\tau) \mathrm{d}\tau \right) }

この式の両辺を時間 tで微分することで、微分方程式

\displaystyle{ \dfrac{\mathrm{d}I(t)}{\mathrm{d}t}=-\dfrac{I(t)}{RC} }

が得られます。 これを解くことで過渡状態における電流が求められます。

初期条件 I(0)=E/R *1と、考えている範囲（ 0 \leq t \lt \Delta t）において常に I(t) \gt 0である*2ことより、微分方程式の解は

\displaystyle{ I(t) = \dfrac{E}{R}\exp\left( -\dfrac{t}{CR} \right) }

となり、過渡状態における電流が求まります。

電圧

電圧はオームの法則とキルヒホッフの法則から求まります。 この２つを考慮すると、コンデンサの両端にかかる電圧は

\displaystyle{ V_C = E - V_R = E - RI(t) }

であることがわかります。

これに先程の電流の式を代入すれば、

\displaystyle{ V_C=E\left( 1 - \exp\left(-\dfrac{t}{CR}\right) \right) }

となり、過渡状態における電圧が求まります。

ちなみに、抵抗による電圧降下は

\displaystyle{ V_R = E\exp\left(-\dfrac{t}{CR}\right) }

とあらわせます。

電荷

過渡状態におけるコンデンサに蓄えられる電荷は、さきほど求めた電圧を使って、

\displaystyle{ Q=CV_C=CE\left( 1 - \exp\left(-\dfrac{t}{CR}\right) \right) }

となります。

t=0と t\to\inftyの極限を考えると、

\displaystyle{ Q(0) = 0 \\ \lim_{t \to \infty}Q(t)=CE }

となっており、過渡状態には電荷が 0から CEまで連続的に変化することがわかります。

*1: t=0において、コンデンサには電圧降下がなく、抵抗では Eの電圧降下があるということです。

*2:充電中にコンデンサ側から電源側に電流が流れることはないということです。