2020-08-06

電圧増幅度と電流増幅度と電力増幅度をhパラメータで表す

電圧増幅度 $A_v$ 、電流増幅度 $A_i$ 、電力増幅度 $A_p$ をトランジスタのhパラメータで表現します。*1 なお、ここではエミッタ接地を前提として話を進めます。つまり、入力電流（電圧）はベース電流（ベース・エミッタ間電圧）のことであり、出力電流（電圧）はコレクタ電流（コレクタ・エミッタ間電圧）のことを指します。

最初に各増幅度とhパラメータの定義を確認します。

電圧増幅度 $A_v$ 、電流増幅度 $A_i$ 、電力増幅度 $A_p$ はそれぞれ、以下のようになります。

$\displaystyle{ A_v=\dfrac{v_o}{v_i} \\ A_i=\dfrac{i_o}{i_i} \\ A_p=\dfrac{p_o}{p_i} \\ }$

hパラメータである出力アドミタンス $h_{oe}$ 、電流増幅率 $h_{fe}$ 、入力インピーダンス $h_{ie}$ 、電圧帰還率 $h_{re}$ の定義はそれぞれ以下のようになります。

$\displaystyle{ h_{oe}=\dfrac{i_o}{v_o} \\ h_{fe}=\dfrac{i_o}{i_i} \\ h_{ie}=\dfrac{v_i}{i_i} \\ h_{re}=\dfrac{v_i}{v_o} }$

以上の式において、 $v_o$ 、 $v_i$ はそれぞれ出力電圧と入力電圧、 $i_o$ 、 $i_i$ はそれぞれ出力電流と入力電流、 $p_o$ 、 $p_i$ はそれぞれ出力電力と入力電力を表します。

電圧増幅度

負荷抵抗が $R_L$ であるとすると、オームの法則から出力電圧は

$\displaystyle{ v_o = R_L i_o }$

と表せます。したがって、電圧増幅度の定義から、

$\displaystyle{ A_v=\dfrac{v_o}{v_i}=\dfrac{R_L i_o}{v_i} }$

となります。

次に、入力インピーダンスを用いれば入力電圧は $v_i=h_{ie}{i_i}$ となるので、

$\displaystyle{ A_v=\dfrac{R_L i_o}{v_i}=\dfrac{R_L i_o}{h_{ie}i_i}. }$

さいごに、出力電流と入力電流を電流増幅率を使って表せば、

$\displaystyle{ A_v=\dfrac{R_L i_o}{h_{ie}i_i}=\dfrac{R_L h_{fe}}{h_{ie}} }$

となり、電圧増幅度をhパラメータ（と負荷抵抗 $R_L$ ）で表せます。

電流増幅度

これはそのまま電流増幅率と一致します。

$\displaystyle{ A_i=\dfrac{i_o}{i_i}=h_{fe} }$

電力増幅度

以前の記事で、電力増幅度は電圧増幅度と電流増幅度の積で表せるという話をしました。

nitomath.hatenablog.jp

そのことを用いれば、

$\displaystyle{ A_p=A_vA_i=\left(\dfrac{R_L h_{fe}}{h_{ie}}\right)h_{fe}=\dfrac{R_L h^2_{fe}}{h_{ie}} }$

とすることで、電力増幅度をhパラメータで表せます。

*1:と言いつつ、出力アドミタンスと電圧帰還率は使用しません。使用するのは電流増幅率と入力インピーダンスだけです。

2020-08-05

トランジスタでLチカする回路の設計手順

npn型トランジスタのコレクタに赤色LEDを繋いでLチカさせるときの回路を設計します。

回路は下図のようなものです。

f:id:nitomath:20200801134351p:plain — トランジスタでLチカする回路

これから順番にそれぞれの値を決めていきます。

トランジスタは2SC1815Y（リンク先は秋月電子です）を使用する想定で設計します（データシートはこちら）。この記事中に載せているすべてのグラフは、このデータシートからの引用です。

電源電圧

電源電圧 $E$ としては、あまり大きすぎない、適当な値を設定してください。私は $E=5~\mathrm{V}$ でやりました。*1

LEDの端子間電圧と電流

まずは回路の上側（コレクタ電流 $I_C$ が流れるところ）から先に決めていきます。

今回の回路では、LEDを流れる電流はコレクタ電流 $I_C$ となります。

赤色LEDを使用する場合は、端子間電圧 $V _{LED}$ を $2~\mathrm{V}$ 程度、LEDを流れる電流 $I_C$ を $20~\mathrm{mA}$ 程度として計算すればいいと思います。*2

コレクタ・エミッタ間電圧

すでにコレクタ電流は決めたので、このグラフをもとにコレクタ・エミッタ間電圧を決めます。

f:id:nitomath:20200801134510p:plain — コレクタ電流とコレクタ・エミッタ間電圧の関係

コレクタ電流は $20~[\mathrm{mA}$ ]としました。そこで、 $I_C=20$ のときの $V_{CE}$ をグラフから読み取ると……ベース電流 $I_B$ がいくつであっても、コレクタ・エミッタ間電圧はほとんど $0~\mathrm{V}$ であることがわかります。*3 *4

ということで、以下では $V_{CE}\fallingdotseq0~[\mathrm{V}$ ]とします。

コレクタ抵抗

続いて、トランジスタのコレクタに繋いでいる抵抗（以下、コレクタ抵抗）の値を決めます。電源電圧 $E$ 、コレクタ抵抗の端子間電圧 $V_{RC}$ 、LEDの端子間電圧 $V_{LED}$ 、コレクタ・エミッタ間電圧 $V_{CE}$ の間には次式の関係が成り立ちます。

$\displaystyle{ E=V _{RC}+V _{LED}+V _{CE} }$

なので、

$\displaystyle{ V _{RC}=E-V _{CE}-V _{LED} }$

となります。

オームの法則（ $V=RI$ ）を使えば、

$\displaystyle{ R_C=\dfrac{V _{RC}}{I _C}=\dfrac{E-V _{CE}-V _{LED}}{I _C} }$

となり、コレクタ抵抗の値を求められます。今回は $E=5~\mathrm{V},~V_{CE}\fallingdotseq0~\mathrm{V},~V_{LED}=2~\mathrm{V},~I_{C}=20~\mathrm{mA}$ なので、計算すると $R_{C}=150~[\mathrm{\Omega}$ ]となります。

ベース電流

続いて、真ん中の回路を流れるベース電流 $I_B$ を決めます。

f:id:nitomath:20200801134435p:plain — 直流電流増幅率とコレクタ電流の関係

上図は直流電流増幅率とコレクタ電流の関係を表したグラフです。

トランジスタを使うのは一般的な部屋の中なので $T_a=25$ として、 $I_C=20$ のときの値を見ると、 $h_{FE}=110$ となっています。ここから、

$\displaystyle{ I_B=\dfrac{I_C}{h_{FE}}=\dfrac{20\times10^{-3}}{110}\fallingdotseq182~[\mathrm{\mu A}] }$

となり、必要なベース電流が求まります。

ベース・エミッタ間電圧

ベース電流を決めた次はベース・エミッタ間電圧 $V_{BE}$ を決めます。*5

f:id:nitomath:20200801134537p:plain — ベース電流とベース・エミッタ間電圧の関係

ベース電流とベース・エミッタ間電圧の関係

上図はベース電流とベース・エミッタ間電圧の関係を表したグラフです。ベース電流を決めたときと同じく、 $T_a=25$ とします。今回は $I_B=182$ なので、グラフをから $V_{BE}=0.7~[\mathrm{V}$ ]程度と決まります。

ベース抵抗

最後に、ベース抵抗の値 $R_B$ を決めます。ベース・エミッタ間電圧が $V_{BE}=0.7$ 、電源電圧が $E=5$ なので、ベース抵抗の端子間電圧 $V_{RB}$ は

$\displaystyle{ V_{RB}=E-V_{BE}=5-0.7=4.3~[\mathrm{V}] }$

となります。

ベース電流が $I_B=182~[\mathrm{\mu A}$ ]であることとオームの法則から、ベース抵抗の値 $R_B$ は

$\displaystyle{ R _B=\dfrac{V_{RB}}{I_{B}}=\dfrac{4.3}{182\times10^{-6}}\fallingdotseq23.6~[\mathrm{k\Omega}] }$

となります。

さいごに

これまでに決めた値を書き込んだ回路図を載せます。

f:id:nitomath:20200801134552p:plain

*1:Arduinoの $5~\mathrm{V}$ ピンを電源として使ったため

*2:データシートがある場合はそれを見て決めてください。私はなかったので本文のような感じでテキトーに決めました。

*3:実際にはコレクタ・エミッタ間飽和電圧なんかを考慮しなければいけないのかもしれない……？

*4: $V_{CE}=0$ で計算してるのは怪しいと思っています。（使ったトランジスタは違うやつだけど）こんな回路を作ったときに $V_{CE}=0.075$ ありましたし。

*5:ここは真面目にやらずに、「ベース・エミッタ間電圧とかだいたい $0.7\sim0.8~\mathrm{V}$ でしょ」くらいでもこの程度の回路ならいいと思います。というか私は面倒だったのでそうしました。

2020-08-04

コンバータとインバータとは何か

日本の家庭用コンセントには $100~\mathrm{V}$ か $200~\mathrm{V}$ の交流が来ています。普段、私達はコンセントにパソコンやスマホを繋いで使用していますが、パソコンやスマホは直流で動作するように作られています。

このように交流電源（コンセント）に直流で動く機器（パソコンやスマホ等）を接続して機器を動かせるのは、電気を交流から直流へ変換する回路が電源と機器の間に存在するからです。

ACアダプタという言葉を聞いたことがあるでしょうか。スマホの充電器でいえばコンセントに挿す、直方体になっているところです。ノートパソコンでいえば、電源コードの途中にある直方体になっているところです。

ACアダプタの内部には交流を直流へと変換する回路が含まれています。*1 そのため、交流が出てくるコンセントと直流で動くスマホやパソコンを接続しても、なんの不自由なくそれらの機器を使うことができます。

このような交流を直流へと変換するものをコンバータと言います。反対に、直流を交流へと変換するものをインバータといいます。

コンバータは、例えばダイオードの整流素子を用いることで交流から直流への変換を実現しています。インバータは、例えばスイッチを用いて出力へ流れる電流の向きを変えることで直流から交流への変換を実現しています。

*1:実際には交流を直流へと変換する回路だけでなく、電圧を下げるためのトランスや電流を安定させる安定化回路も含まれます

2020-08-03

「電圧はかかっているが電流は流れていない状態」を実際に計測する

下図のような回路（？）があるとします。*1

f:id:nitomath:20200725121003p:plain — 不完全な回路

このとき、点Bと点Cの電圧は $E~[\mathrm{V}$ ]ですが、これらの点を流れている電流は $0~\mathrm{A}$ です。このように、「電圧が $0$ でなくとも、電流が流れないことがある」ということを知識としては知っていますが、実際にこのような回路で計測したことはありませんでした。

ということで、実際に計測をして「電圧が $0$ でなくとも、電流が流れないことがある」ことを確かめてみました。

適当な回路を組んでBC間の電位差（抵抗の端子間電圧）を計測した結果が次の画像です。電源電圧は $E=1~[\mathrm{V}$ ]としました。

f:id:nitomath:20200725120959j:plain — 抵抗の端子間電圧（BC間の電圧）は0Vだった。

結果は $0~\mathrm{V}$ ！オームの法則より、抵抗の端子間電圧が $0~\mathrm{V}$ ということは抵抗を流れている電流は $0~\mathrm{A}$ であると言えます！つまり、電流は流れていない！！

……至極当然のことを確かめる結果となりました。しかし、理論や知識として知っていることを実際に確かめるのは楽しいです。

おまけ

AC間の電圧が $1~\mathrm{V}$ であることを確かめています。

f:id:nitomath:20200725120950j:plain — AC間の電位差は1Vだった。

*1:繋がっていないので回路と呼べるのかわかりませんが、なんと呼べばいいのかわからないのでとりあえずこの記事では回路で通します。

2020-08-02

電力増幅度は電流増幅度と電圧増幅度の積になる

電流増幅度 $A_i$ は、入力電流を $i_i$ 、出力電流を $i_o$ とすると、

$\displaystyle{ A_i = \dfrac{i_o}{i_i} }$

と表せます。

電圧増幅度 $A_v$ は、入力電圧を $v_i$ 、出力電圧を $v_o$ とすると、

$\displaystyle{ A_v = \dfrac{v_o}{v_i} }$

と表せます。

電力増幅度 $A_p$ は、入力電力を $p_i$ 、出力電力を $p_o$ とすると、

$\displaystyle{ A_p = \dfrac{p_o}{p_i} }$

と表せます。

電力は電流と電圧の積（ $p=iv$ ）なので、電力増幅度は、

$\displaystyle{ A_p = \dfrac{p_o}{p_i}=\dfrac{i_ov_o}{i_iv_i}=A_iA_v }$

というふうに、電流増幅度と電圧増幅度の積で表せます。

このことは当たり前といえば当たり前ですが、知ったとき、個人的には「整合性が取れているな」と感じました。

2020-08-02

回路のデッドタイムとはなにものか

４個のスイッチ（ $S_1,~S_2,~S_3,~S_4$ ）を使ったHブリッジ回路について考えます。スイッチは左上が $S_1$ 、右上が $S_2$ 、左下が $S_3$ 、右下が $S_4$ とします。

f:id:nitomath:20200724103943p:plain — Hブリッジ回路

Hブリッジ回路はDCモータを駆動するために使われる回路です。*1 DCモータを回転させているとき、回路は次の２つの状態を取ります。

$S_1$ と $S_4$ がON。 $S_2$ と $S_3$ がOFF。（モータ正転）
$S_1$ と $S_4$ がOFF。 $S_2$ と $S_3$ がON。（モータ逆転）

この２つの状態を切り替えるとき（例えば、正転させていたモータを逆転させるとき）、デッドタイムというすべてのスイッチがOFFになっている時間を設ける必要があります。回路が短絡（ショート）し、大きな電流（貫通電流）が流れるのを防ぐためです。

回路が短絡するのは高電位側と低電位側が直接繋がったときです。モータの正転と逆転を切り替えるとき、一瞬でも

$S_1$ と $S_3$ がONになるか、
$S_2$ と $S_4$ がONになるか、
両方が同時に起きる

とモータを通らないルートができてしまうため、回路が短絡し、貫通電流が発生します。

*1:モータを一方向に回転させたいだけならHブリッジ回路は必要ありません。モータを二方向に回転させたい（正転・逆転させたい）となると必要になります。

2020-07-30

RC回路におけるコンデンサ充電時の電流、電圧、電荷を求める

この記事では、起電力 $E$ の電源、スイッチ、静電容量 $C$ のコンデンサ、抵抗値 $R$ の抵抗が直列接続された回路（RC直列回路）を考えます。そして、過渡状態における回路を流れる電流、コンデンサの両端にかかる電圧、コンデンサに蓄えられる電荷を求めます。

f:id:nitomath:20200723100727p:plain — RC直列回路

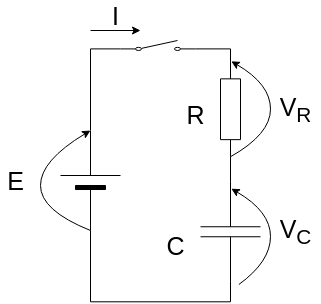
時刻 $t=0$ でスイッチをONにします。そのとき、電荷 $Q=CE$ がコンデンサに一瞬で蓄えられるわけではありません。つまり、コンデンサに蓄えられている電荷は

$\displaystyle{ Q= \begin{cases} 0~\left( t \lt 0 \right) \\ CE~\left( 0 \leq t \right) \end{cases} }$

という式では表せません。

実際には、スイッチがONになってから $\Delta t$ の間、蓄えられている電荷が $0$ から $CE$ にまで連続的に変化する期間（過渡状態）があります。つまり、

$\displaystyle{ Q= \begin{cases} 0~\left( t \lt 0 \right) \\ Q\left(t\right)~\left( 0 \leq t \lt \Delta t\right) \\ CE~\left( \Delta t \leq t \right) \\ \end{cases} }$